如果一把枪里有100万个枪膛位,但里面却只有一发子弹。你问我要多少钱才肯用它朝自己开一枪?我告诉你,给我多少钱我也不干!

先来看一道简单的掷骰子问题:
给你两颗骰子(当然每个骰子6个面),问当两个骰子掷出的数字和大于10的概率有多大?
这是一道非常简单的概率题,我们唯一需要注意的是,针对每一个sum(比如10),可能有多种组合(比如4+6, 5+5),因此,我们这里只需要简单穷举一下即可:
| 两个骰子的总和 | 所有可能的组合数 |
|---|---|
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 5 |
| 7 | 6 |
| 8 | 5 |
| 9 | 4 |
| 10 | 3 |
| 11 | 2 |
| 12 | 1 |
所有可能情况的总和是36(1+2+3+4+5+6+5+4+3+2+1),针对大于10的情况是掷出11和12,那么一共有3种(5-6,6-5,6-6)。所以上面问题的答案就是:P(n|n>10)=1/12。
以上问题非常简单,有点概率基础的人都可以轻易搞定。这里,如果我们更进一步,将这个问题抽象如下:
给定n个色子(n>=1),每个骰子有m个面,每一个面的点数分别表示为1到m(比如m=10个面,那么这10个面的点数分别是1,2,3….10)。给定一个sum,表示一次投掷n个骰子的所有正面数字总和。那么你给定一个数x,如果sum>x则表示你赢了,那么问你赢的概率有多大?
一旦抽象化以后,就会发现,上面那道简单问题实际上是此问题的一种特殊情况(n=2,m=6,x=10)。
如何解决这个问题?我们先将上面的文字语言描述,转换为数学语言描述:
- 设投掷n个m面筛子正面总和大于x的事件为A
- P(A)即为所求问题的解
- 每个面出现是等可能事件,即概率为1/m
- P(sum=i)表示掷出正面总和为i的概率
那么问题转换为:
$$P(A) = \sum_{i=1+x}^{m*n}{P(sum=i)}$$
上面公式表示的意思是,如果我们想赢得游戏,只需要分别计算出掷出总和大于给定x的概率即可;比如我们给定向量对 < n=2,m=6,x=10 > 那么想要赢得游戏,我们需要知道掷出11和12的概率分别是多少,把他们相加,就是我们能够赢的概率了,即P(sum=10+1=11)+P(sum=10+2=12)的概率。
那么下一步我们如何计算$P(sum=i)$的概率呢?即计算给定n个m面色子,掷出正面总和为i的概率。这里就需要借助递归的思想。我们设如下函数:$f(n,m,x)$ 表示n个m面骰子掷出总和为x的所有可能的组合数(想一下文章开头的那个例子)。我们假设这个时候其中有一个色子掷出了k(1<=k<=m),那么剩下的骰子(n-1),就需要掷出总和为x-k。因此递归表示法:
$$f(n,m,x)=\sum_{k=1}^{m}{f(n-1,m,x-k)}(n>1,1<=k<=m)$$
递归终止条件为n=1,即当n=1的时候,如果x>m则函数为0,x<=m则为1:
$$f(1,m,x)=1(1<=x<=m)$$
此时,我们就能够通过递归的方式,求出f(n,m,x)函数了。有了f函数,那么一切顺其自然的得到$P(sum=i)$ ,表示如下:
$$P(sum=i)=f(n, m, i)/\sum_{j=1}^{m*n}{f(n, m, j)}$$
我们可以看到$\sum_{j=1}^{m*n}{f(n, m, j)}$针对每一个$P(sum=i)$都是相同的,因此只需要计算一次即可,他表示所有的可能值的总和。
因此通过上面的推到,所求问题最后就变成了如下公式:
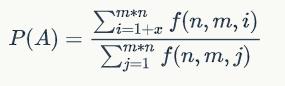
有了公式和上面的推理,我们就能够通过代码来解决该问题了。
f函数的代码如下:
|
同理,我们也很容易求得f(n,m,x+1) f(n,m,x+2) ... f(n,m,m*n),即大于x的所有可能情况:
|
因此最后的代码为:
|
后记
这道题实际上并不难,主要是考察我们能否具有抽象思维和发散思维。对于一般性问题,我们能够将它推广到更加一般的情况吗?抽象思维至关重要。
有些人说了,当m<=3的时候,是不存在的,m=4的锥面体,每个面被掷到的概率也不是1/4。我们其实大可不必追究这些现实问题,只需要去抽象成一般情况即可。